The Roberval Balance.

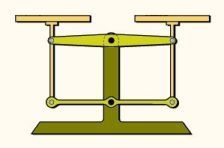
Double-pan laboratory balance.
Though many students have never heard of the Roberval balance, most have used one. The standard laboratory double-pan balance has a Roberval construction that keeps the pans level as they move up and down. More importantly, it prevents the pans from rotating as they move up and down, and this is the principle that ensures that the position of weights on the pans has no effect on the balance.

This may not seem remarkable, but consider the simple lever. The position of the weights on a lever (balance-bar) relative to the fulcurm is what determines balance. Many scales used for weighing have one such bar with a sliding weight. (Even the laboratory double-pan balance incorporates such a sliding weight for fine adjustment.)

 

Hanging-pan scales.
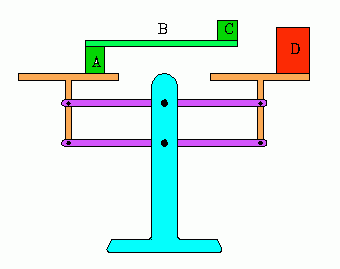Do students really understand the various forms of balance? I doubt it. In addition to the two mentioned above, there's the balance scale with two suspended pans. Again, the position of weights on the pans doesn't matter, but for an entirely different reason. In this scale, each pan moves and tilts to find an equilibrium position so that the center of mass of pan and weight is directly under the suspension point.

 

Surprising demo with the Roberval balance.
The Roberval balance is a compound lever system. Students who try to treat it as nothing more than a simple lever get into serious trouble. Consider the example shown to the left. The red weight D is on the right pan. The green weights A, B, and C are fastened or glued together and to the pan so that some of the weight is on the right of the central pivot of the balance. No matter. So long as A + B + C = D, the system is in balance.

The Roberval balance achieves non-rotation of the pans by use of a parellogram linkage of levers. This is a special case of the "pantograph" lever system used for copying drawings to larger or smaller size. But other systems may be used to achieve the same result, for example, gears or pulleys.

When Roberval invented this balance, many persons, including mechanics, had only superficial understanding of mechanical principles. The demo illustrated here would surprise them, for they simplistically thought that balance was determined solely on weight and distance from the rotation axis of the scales. Many perpetual motion machine inventors still thought that if there was more weight on one one side of a system's rotation axis, then the system could not be in equilibrium, and therefore must rotate. This simple demonstration clearly shows that is not so.

 

Overbalanced chain. Doesn't move. Very overbalanced system.

These two examples should convince anyone. But inventors still continue to make these same mistakes.

 

Gear balance, behaves like a Roverval balance.

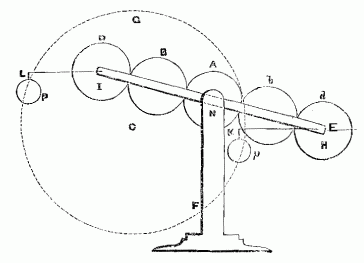
We said that a balance on the Roberval principle could be made with gears. Here's an example. Five gears are on a rigid beam IH. The bar is free to rotate about the central axis on the support pedestal. The gears rotate, except for the center one that is fastened to the pedestal and cannot move. Horizontal arms LI and KE remain horizontal at all times, for they are fastened to the gears at each end of the main beam IH. Therefore the equal mass round weights P and p can be placed anywhere on these arms and the system is still in balance. In fact, if the bars KE were made extremely long both weights could be on the left side of the central axis. They could be directly above or below each other, or p could even be to the left of P. The system would still be in balance.

The weights on the pans of a pan balance are adjusted to equality. Fine adjustment is accomplished with a simple lever scale incorporated into the instrument. A Roberval linkage could be made to balance unequal masses, or to balance for a particular ratio of masses, say 1:10.

Thinking about these systems leads us to reformulate our ideas about balances. The law of the lever is, Aa = Bb where A and B are masses on lever arms a and b. The lever arms are the lengths from the centers of mass of A and B to the rotation axis. But we can also interpret a and b to be the radii of the arcs of the motion of A and B as the system moves near the equilibrium point.

The pans of a Roberval balance move in such a way that the radius of the arc of motion of a weight is independent of its position of the weight on the pan. Wherever the weight is placed on the pan, it moves the same vertical distance. That's the "Roberval principle" common to all of these kinds of balance.